
Hoy en día, la seguridad en las comunicaciones a través de internet, y otras tecnologías, requieren para su funcionamiento encontrar números primos de gran cantidad de cifras. Pero más allá de los ordenadores, la caza de primos, cantidades únicamente divisibles entre sí mismas y la unidad, ha sido uno de los desafíos matemáticos que más pasiones ha levantado a lo largo de la historia. Euclides, en torno al 300 antes de Cristo, ya relacionó los llamados números perfectos, que son iguales a la suma de sus divisores propios (como el 6; 6 = 1 + 2 + 3), con números primos de la forma 2^p - 1 (siendo p un número primo).
Unos cuantos siglos después, esta misma expresión fue propuesta por el filósofo, matemático y sacerdote francés Marin Mersenne (1588-1648) con el objetivo de producir números primos. Mersenne, que falleció hace 370 años un 1 de septiembre, estudió teología, matemáticas y teoría musical. Tras intentar, sin éxito, hallar una fórmula que describiera a todos los primos, se dedicó a estudiar la expresión M(n) = 2^n - 1, con n un número natural. Aunque no produce primos para cualquier valor de n (de hecho, cuando n es compuesto, M(n) siempre es compuesto), de forma bastante recurrente sí lo hace. Los números primos que se pueden expresar de esta manera se llaman primos de Mersenne. En 1641, Mersenne enunció en su obra Cogitata physico-mathematica que cuando n es un primo menor o igual que 257, solo los números M(2), M(3), M(5), M(7), M(13), M(17), M(19), M(31), M(67), M(127) y M(257) eran primos. Sin embargo, esta lista no era correcta: M(67) y M(257) son en realidad compuestos, mientras que faltan los primos M(61), M(89) y M(107).

Se ha especulado mucho sobre el método que siguió Mersenne para escoger su lista y parece que consideró que M(p) era primo siempre que p se pudiera escribir como 2^k + 1, 2^k - 1, 4^k + 3 o 4^k - 3 (siendo k un número natural), y viceversa. Sin embargo, este criterio no explicaba la omisión del caso M(61), que lo cumple para k = 3 (61 = 4^3 - 3). Esto podría deberse a que Mersenne creyó erróneamente que era compuesto, o más probablemente a un error tipográfico a la hora de escribir la lista.
La búsqueda de una explicación para la lista de Mersenne llevó a la llamada nueva conjetura de Mersenne, que sostiene que si dos de las tres condiciones siguientes son ciertas, también lo es la tercera: 1) M(p) es primo; 2) p = 2^k + 1; 2^k - 1; 4^k + 3 o 4^k - 3; 3) (2^p + 1) / 3 es primo. Hoy en día se continúa el estudio de esta conjetura con ayuda de ordenadores. También se emplea la capacidad de cálculo de los ordenadores para encontrar primos de Mersenne cada vez más grandes. Hasta la fecha se conocen 50, siendo el mayor M(77232917), con más de 23 millones de cifras. Sin embargo, no se sabe si, tal y como le ocurrió a Mersenne, se está omitiendo algún primo más pequeño por el camino.
A lo largo de la historia se han empleado otras fórmulas para generar primos. En 1772, Leonhard Euler observó que la expresión P(n) = n^2 + n + 41 generaba primos para n = 0, 1, 2, …, 39, pero a partir de 40 comienzan a aparecer también números compuestos. Estas expresiones polinómicas son más simples de manejar que las que involucran potencias, como la de Mersenne, pero su potencia es limitada, ya que ningún polinomio P(n) con coeficientes enteros genera primos para todos los valores de n.
Considerando polinomios con más variables, del tipo P(x, y)= 2x^2 +3xy + y^7 +8, se obtienen fórmulas sorprendentes, como la que se desprende del famoso teorema de Matiyasevich en el que da la solución a uno de los problemas planteados por Hilbert sobre ecuaciones diofánticas. En 1976 un grupo de matemáticos empleó este teorema para afirmar que los valores positivos de la expresión que aparece en la imagen de abajo son todos los primos. Pero comprobar esto de forma efectiva es una tarea impracticable, ya que dando valores de 0 a infinito a las variables, en su inmensa mayoría se obtienen números negativos.
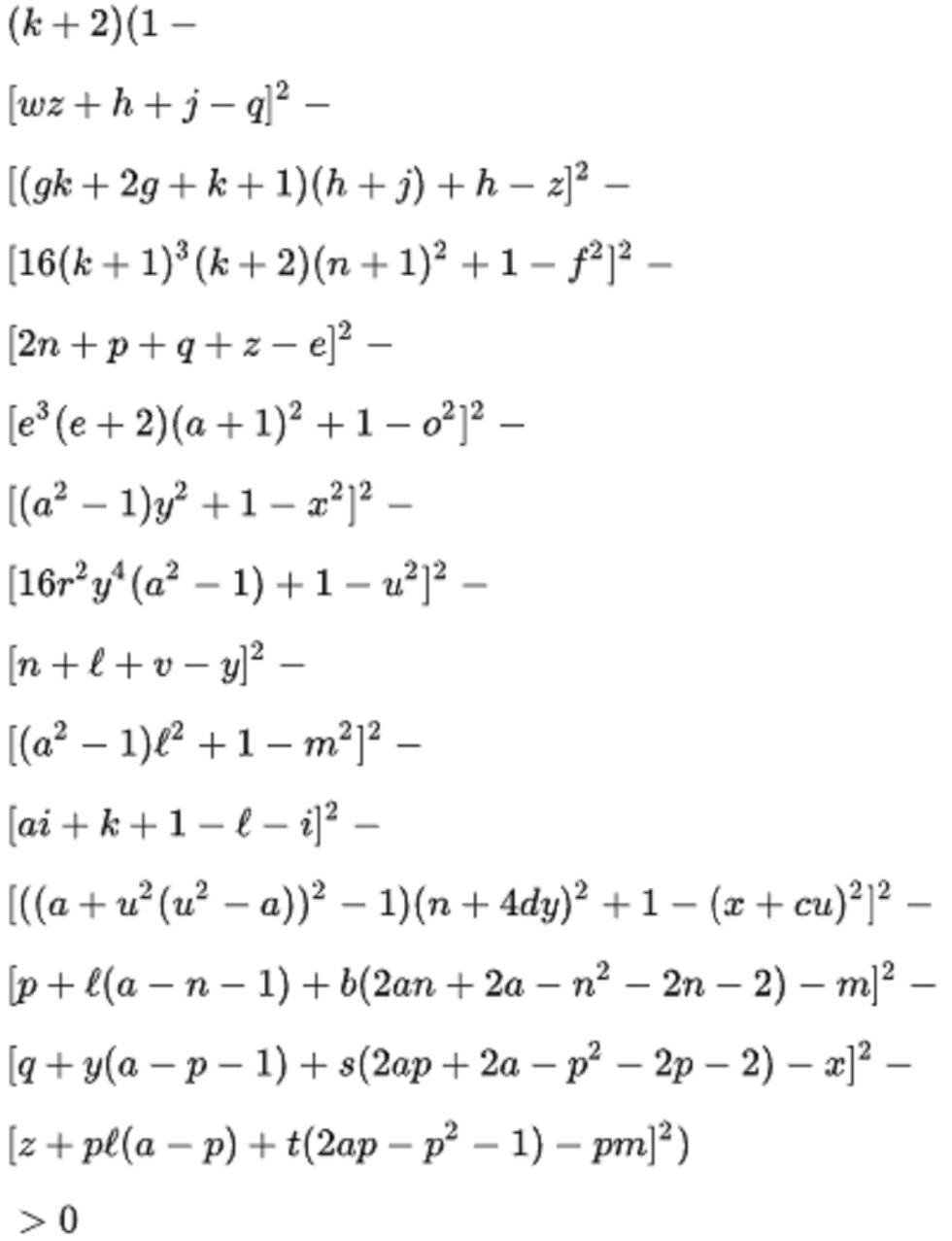
¿Podría haber entonces alguna fórmula sencilla que los generara todos, como pretendía Mersenne? Existen algunas que rastrean los números naturales y localizan automáticamente los números primos. Por ejemplo, la fórmula de Wilson que aparece en la segunda imagen genera para cada n el valor n + 1 si n + 1 es primo y el valor 2 si no lo es. Aunque es mucho más sencilla que la fórmula anterior, resulta poco práctica, ya que su coste de cálculo es muy elevado. En general, cuantos más casos contemplan (más números primos producen) las fórmulas, más ineficientes computacionalmente resultan. Así que por el momento, seguiremos buscando una máquina más eficiente que ayude a generar primos.
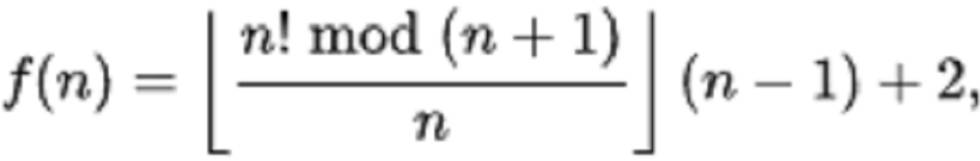
José Granados es estudiante de doctorado en matemáticas de la Universidad Autónoma de Madrid y miembro del ICMAT.
Edición y coordinación: Ágata Timón (ICMAT)
