
El binomio “matemáticas y flamenco” genera todo tipo de reacciones. Matemáticos, académicos, periodistas, docentes, artistas, aficionados y público en general manifiestan su parecer en cuanto oyen las dos palabras unidas. No en vano, nuestro trabajo ha suscitado un impacto mediático no usual para las investigaciones matemáticas que puede constatarse sin más que poner “matemáticas y flamenco” en un buscador web.

Quizás se deba, entre otras razones, a los tópicos que ambas palabras sufren, ya que las dos disciplinas están asignadas a segmentos muy reducidos de la sociedad, una etiquetada como fría y distante (“solo para súperinteligentes”), la otra como pasional y festera, ambas como ininteligibles.
En cualquier caso, cuando alguien muestra interés en conocer el por qué del mágico binomio, tras explicarle en una frase el asunto, cae rendido inmediatamente ante la evidencia. “¡Claro, el flamenco es música y las matemáticas herramientas que pueden usarse!” expresa sorprendido el interesado.
Una vez superados la desconfianza y el miedo o grima que supone para un matemático invertir tiempo en este tema, pues no se suele considerar serio, profundo o interesante a primera vista, podemos pasar a introducir algunas ideas sobre este asunto.
La relación entre la música y las matemáticas es natural e incuestionable. Desde la antigua Grecia (donde se establecieron los pilares fundamentales del conocimiento), la música no sólo se consideró como una expresión artística de las matemáticas sino que su estudio y análisis estuvo siempre ligado a la teoría de números. De hecho, matemáticos de todas las épocas han hecho de la música su objeto de estudio y, en la actualidad, tanto en revistas de música como de matemáticas o en Internet, pueden encontrarse multitud de documentos en los que se utilizan teorías matemáticas para el análisis musical o la composición de obras musicales. Además, muchos estudios de la música han dado lugar a retos matemáticos que han supuesto un avance o creación de nuevas área de investigación. Por otra parte, existen hoy en día propuestas del uso de la música en las clases de matemáticas en distintos niveles educativos, así como de la utilización de aplicaciones tecnológicas en las clases de música. Por tanto, la interacción de estas dos disciplinas supone un caso claro de transferencia del conocimiento desde la universidad a la sociedad.
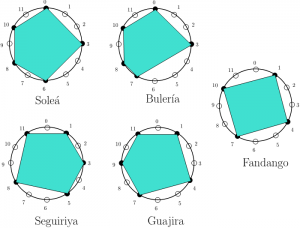
Dicho esto, exponemos en esta entrega una muestra de lo que puede ocurrir si nos atrevemos a usar matemáticas para estudiar la música del flamenco. Lo primero que hemos de hacer es modelar el problema que queremos estudiar, en este caso mencionamos el problema de la búsqueda de ritmos que posean ciertas propiedades. En la figura adjunta se ilustra la representación poligonal de algunos ritmos del flamenco. El punto de partida considerar los doce pulsos del compás(metro rítmico) como puntos equidistantes en una circunferencia de forma que podemos imaginar un collar de perlas blancas (acentos débiles) y negras (acentos fuertes) en forma o diagrama de reloj. Esto tiene sentido porque el compás se repite en el tiempo (o sea, es una función periódica). Si unimos cada dos acentos fuertes consecutivos del compás nos aparece el polígono cuyos vértices son precisamente esas perlas negras. En la representación poligonal el “1” marca la posición en la cual comienza el patrón rítmico y los vértices indican dónde están los acentos. Podemos ver y oír los distintos compases flamenco aquí.
Una de las propiedades que los musicólogos y matemáticos han observado en distintas músicas de tradición oral es la denominada regularidad del ritmo (o de la escala musical). Los ritmos regulares son aquellos que maximizan cierta medida geométrica. Por ejemplo, atendiendo a la representación poligonal de un ritmo, podemos considerar como medida de regularidad la suma de las distancias entre cada par de acentos (perlas negras del collar) o bien, el área del polígono rítmico.

Este tipo de problemas involucra campos matemáticos como la combinatoria y la geometría y han sido tratados por los matemáticos desde hace bastante tiempo. En 1956, el matemático húngaro F. Tóth estudia el caso continuo y prueba que un conjunto de n puntos sobre un círculo que maximizan la suma de las distancias entre cada par de puntos se encuentra precisamente en los vértices de un polígono regular de nlados. Dicho de otro modo, los vértices están distribuidos tan regularmente como sea posible. Con respecto al criterio de máxima área, usando geometría elemental puede probarse que para n=3 puntos se cumple que el triángulo de área máxima inscrito en un círculo es el equilátero. Usando argumentos geométricos, puede probarse también el caso general, esto es, el polígono de n vértices inscrito en un círculo que maximiza el área es un polígono regular (cuadrado para n=4, pentágono regular para n=5, etc.).
El caso que nos ocupa en la música corresponde a lo que llamamos la versión discreta del problema, esto es, la elección de los vértices del polígono se hace sobre un conjunto finito de puntos fijados de antemano (los 12 tiempos). El problema discreto general se formula así:
Problema 1: Polígono de máxima área. Considera n puntos uniformemente distribuidos en una circunferencia. Determina cómo elegir k<n de esos puntos de forma que el polígono que generan los k vértices sea de área máxima.
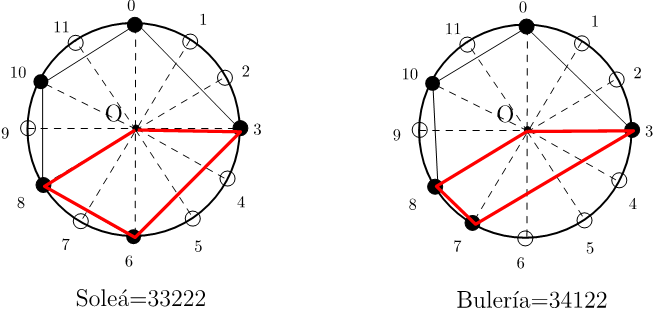
En el caso de los ritmos flamencos tenemos n=12 y k=4 (fandango) o k=5 (soleá, bulería, seguiriya y guajira). Dejamos propuesta al lector la prueba formal de que el polígono que representa el compás de soleá es el pentágono de máxima área. Como ayuda damos la Figura 2, ilustrando que la distribución de 5 puntos elegidos de entre los 12 dados puede ser codificada por un vector que indique la cantidad de triángulos idénticos que hay entre cada dos puntos (acentos) consecutivos. Por ejemplo, la soleá puede denotarse como 33222 y la bulería como 34122.
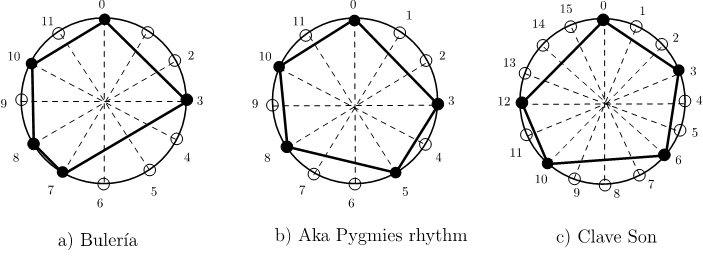
Para los lectores que consideren interesante el problema anterior, damos un paso más y proponemos aquí otro problema o reto matemático. Como hemos mencionado, el ritmo que hemos etiquetado bulería (que se suele ejecutar en las bulerías por soleá) no es de máxima área. Sin embargo, atesora otra propiedad geométrica: no contiene vértices antipodales (diametralmente opuestos). Nos preguntamos si esta propiedad es exclusiva del flamenco y hemos observado que ritmos que han tenido trascendencia en otras culturas también la poseen. En la figura lateral aparecen tres patrones rítmicos que representan a tres grandes culturas musicales: aparte de la bulería en el flamenco, tenemos un ritmo de los Pigmeos Aka (véase un ejemplo aquí), cuya música también está reconocida por la UNESCO, al igual que el flamenco, como herencia cultural intangible de la humanidad y la clave del son, que constituye la base de la música salsa que se baila en casi todos los países y ha conquistado el mundo.
Está claro entonces que esta propiedad rítmica de no contener vértices antipodales puede ser de preferencia cultural y podemos estudiarla desde las matemáticas. Esta propiedad, que produce cierta asimetría perceptual, puede expresarse equivalentemente como que no podamos dividir el círculo en dos mitades iguales usando un segmento que conecta a dos vértices del polígono y requiere que el círculo esté dividido en un número par de arcos (12 en el caso que nos ocupa). El etnomusicólogo Simha Arom la llamó “rhythmic oddity” y se ha estudiado desde las matemáticas (véase las referencias en [1,2]) dando lugar a distintos problemas de optimización discreta. En particular, inspirados en el caso de la bulería por soleá, podemos finalizar planteando el problema geométrico siguiente:
Problema 2: Polígono sin vértices antipodales de máxima área. ¿Cuál es el pentágono sin vértices antipodales de máxima área inscrito en el polígono regular de 12 vértices? ¿Corresponde a algún ritmo musical?

Referencias:
- [1] J. M. Díaz-Báñez , Sobre problemas de matemáticas en el estudio de la música flamenca, La Gaceta de la Real Sociedad Matemática Española, 13, 3, 513-541, 2013.
- [2] J.M. Díaz-Báñez, Mathematics and Flamenco: An Unexpected Partnership, The Mathematical Intelligencer, 39(3), 27-39, 2017.
- Portal electrónico del Proyecto COFLA donde pueden encontrarse artículos, audios y videos ilustrativos.
